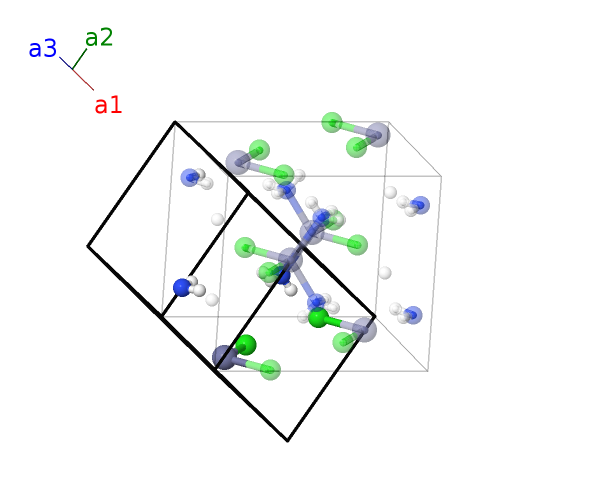
Zn(NH$_{3}$)$_{2}$Cl$_{2}$ ($E1_{2}$) Structure: A2B6C2D_oI44_74_i_hj_h_e-001
| Prototype | Cl$_{2}$N$_{2}$H$_{6}$Zn |
| AFLOW prototype label | A2B6C2D_oI44_74_i_hj_h_e-001 |
| Strukturbericht designation | $E1_{2}$ |
| ICSD | 140642 |
| Pearson symbol | oI44 |
| Space group number | 74 |
| Space group symbol | $Imma$ |
| AFLOW prototype command |
aflow --proto=A2B6C2D_oI44_74_i_hj_h_e-001
--params=$a, \allowbreak b/a, \allowbreak c/a, \allowbreak z_{1}, \allowbreak y_{2}, \allowbreak z_{2}, \allowbreak y_{3}, \allowbreak z_{3}, \allowbreak x_{4}, \allowbreak z_{4}, \allowbreak x_{5}, \allowbreak y_{5}, \allowbreak z_{5}$ |
Other compounds with this structure
Zn(NH$_{3}$)$_{2}$Br$_{2}$
- (Ivšić, 2019) studied this system at 100K and were able to located the hydrogen atoms. The positions of the other atoms are similar to those in earlier works such as (Yamaguchi, 1981) and the space group is unchanged, so we use this as the prototype for the $E1_{2}$ label.
\[ \begin{array}{ccc}
\mathbf{a_{1}}&=&- \frac{1}{2}a \,\mathbf{\hat{x}}+\frac{1}{2}b \,\mathbf{\hat{y}}+\frac{1}{2}c \,\mathbf{\hat{z}}\\\mathbf{a_{2}}&=&\frac{1}{2}a \,\mathbf{\hat{x}}- \frac{1}{2}b \,\mathbf{\hat{y}}+\frac{1}{2}c \,\mathbf{\hat{z}}\\\mathbf{a_{3}}&=&\frac{1}{2}a \,\mathbf{\hat{x}}+\frac{1}{2}b \,\mathbf{\hat{y}}- \frac{1}{2}c \,\mathbf{\hat{z}}
\end{array}\]
Basis vectors
| Lattice coordinates | Cartesian coordinates | Wyckoff position | Atom type | |||
|---|---|---|---|---|---|---|
| $\mathbf{B_{1}}$ | = | $\left(z_{1} + \frac{1}{4}\right) \, \mathbf{a}_{1}+z_{1} \, \mathbf{a}_{2}+\frac{1}{4} \, \mathbf{a}_{3}$ | = | $\frac{1}{4}b \,\mathbf{\hat{y}}+c z_{1} \,\mathbf{\hat{z}}$ | (4e) | Zn I |
| $\mathbf{B_{2}}$ | = | $- \left(z_{1} - \frac{3}{4}\right) \, \mathbf{a}_{1}- z_{1} \, \mathbf{a}_{2}+\frac{3}{4} \, \mathbf{a}_{3}$ | = | $\frac{3}{4}b \,\mathbf{\hat{y}}- c z_{1} \,\mathbf{\hat{z}}$ | (4e) | Zn I |
| $\mathbf{B_{3}}$ | = | $\left(y_{2} + z_{2}\right) \, \mathbf{a}_{1}+z_{2} \, \mathbf{a}_{2}+y_{2} \, \mathbf{a}_{3}$ | = | $b y_{2} \,\mathbf{\hat{y}}+c z_{2} \,\mathbf{\hat{z}}$ | (8h) | H I |
| $\mathbf{B_{4}}$ | = | $\left(- y_{2} + z_{2} + \frac{1}{2}\right) \, \mathbf{a}_{1}+z_{2} \, \mathbf{a}_{2}- \left(y_{2} - \frac{1}{2}\right) \, \mathbf{a}_{3}$ | = | $- b \left(y_{2} - \frac{1}{2}\right) \,\mathbf{\hat{y}}+c z_{2} \,\mathbf{\hat{z}}$ | (8h) | H I |
| $\mathbf{B_{5}}$ | = | $\left(y_{2} - z_{2} + \frac{1}{2}\right) \, \mathbf{a}_{1}- z_{2} \, \mathbf{a}_{2}+\left(y_{2} + \frac{1}{2}\right) \, \mathbf{a}_{3}$ | = | $b \left(y_{2} + \frac{1}{2}\right) \,\mathbf{\hat{y}}- c z_{2} \,\mathbf{\hat{z}}$ | (8h) | H I |
| $\mathbf{B_{6}}$ | = | $- \left(y_{2} + z_{2}\right) \, \mathbf{a}_{1}- z_{2} \, \mathbf{a}_{2}- y_{2} \, \mathbf{a}_{3}$ | = | $- b y_{2} \,\mathbf{\hat{y}}- c z_{2} \,\mathbf{\hat{z}}$ | (8h) | H I |
| $\mathbf{B_{7}}$ | = | $\left(y_{3} + z_{3}\right) \, \mathbf{a}_{1}+z_{3} \, \mathbf{a}_{2}+y_{3} \, \mathbf{a}_{3}$ | = | $b y_{3} \,\mathbf{\hat{y}}+c z_{3} \,\mathbf{\hat{z}}$ | (8h) | N I |
| $\mathbf{B_{8}}$ | = | $\left(- y_{3} + z_{3} + \frac{1}{2}\right) \, \mathbf{a}_{1}+z_{3} \, \mathbf{a}_{2}- \left(y_{3} - \frac{1}{2}\right) \, \mathbf{a}_{3}$ | = | $- b \left(y_{3} - \frac{1}{2}\right) \,\mathbf{\hat{y}}+c z_{3} \,\mathbf{\hat{z}}$ | (8h) | N I |
| $\mathbf{B_{9}}$ | = | $\left(y_{3} - z_{3} + \frac{1}{2}\right) \, \mathbf{a}_{1}- z_{3} \, \mathbf{a}_{2}+\left(y_{3} + \frac{1}{2}\right) \, \mathbf{a}_{3}$ | = | $b \left(y_{3} + \frac{1}{2}\right) \,\mathbf{\hat{y}}- c z_{3} \,\mathbf{\hat{z}}$ | (8h) | N I |
| $\mathbf{B_{10}}$ | = | $- \left(y_{3} + z_{3}\right) \, \mathbf{a}_{1}- z_{3} \, \mathbf{a}_{2}- y_{3} \, \mathbf{a}_{3}$ | = | $- b y_{3} \,\mathbf{\hat{y}}- c z_{3} \,\mathbf{\hat{z}}$ | (8h) | N I |
| $\mathbf{B_{11}}$ | = | $\left(z_{4} + \frac{1}{4}\right) \, \mathbf{a}_{1}+\left(x_{4} + z_{4}\right) \, \mathbf{a}_{2}+\left(x_{4} + \frac{1}{4}\right) \, \mathbf{a}_{3}$ | = | $a x_{4} \,\mathbf{\hat{x}}+\frac{1}{4}b \,\mathbf{\hat{y}}+c z_{4} \,\mathbf{\hat{z}}$ | (8i) | Cl I |
| $\mathbf{B_{12}}$ | = | $\left(z_{4} + \frac{1}{4}\right) \, \mathbf{a}_{1}- \left(x_{4} - z_{4}\right) \, \mathbf{a}_{2}- \left(x_{4} - \frac{1}{4}\right) \, \mathbf{a}_{3}$ | = | $- a x_{4} \,\mathbf{\hat{x}}+\frac{1}{4}b \,\mathbf{\hat{y}}+c z_{4} \,\mathbf{\hat{z}}$ | (8i) | Cl I |
| $\mathbf{B_{13}}$ | = | $- \left(z_{4} - \frac{3}{4}\right) \, \mathbf{a}_{1}- \left(x_{4} + z_{4}\right) \, \mathbf{a}_{2}- \left(x_{4} - \frac{3}{4}\right) \, \mathbf{a}_{3}$ | = | $- a x_{4} \,\mathbf{\hat{x}}+\frac{3}{4}b \,\mathbf{\hat{y}}- c z_{4} \,\mathbf{\hat{z}}$ | (8i) | Cl I |
| $\mathbf{B_{14}}$ | = | $- \left(z_{4} - \frac{3}{4}\right) \, \mathbf{a}_{1}+\left(x_{4} - z_{4}\right) \, \mathbf{a}_{2}+\left(x_{4} + \frac{3}{4}\right) \, \mathbf{a}_{3}$ | = | $a x_{4} \,\mathbf{\hat{x}}+\frac{3}{4}b \,\mathbf{\hat{y}}- c z_{4} \,\mathbf{\hat{z}}$ | (8i) | Cl I |
| $\mathbf{B_{15}}$ | = | $\left(y_{5} + z_{5}\right) \, \mathbf{a}_{1}+\left(x_{5} + z_{5}\right) \, \mathbf{a}_{2}+\left(x_{5} + y_{5}\right) \, \mathbf{a}_{3}$ | = | $a x_{5} \,\mathbf{\hat{x}}+b y_{5} \,\mathbf{\hat{y}}+c z_{5} \,\mathbf{\hat{z}}$ | (16j) | H II |
| $\mathbf{B_{16}}$ | = | $\left(- y_{5} + z_{5} + \frac{1}{2}\right) \, \mathbf{a}_{1}- \left(x_{5} - z_{5}\right) \, \mathbf{a}_{2}- \left(x_{5} + y_{5} - \frac{1}{2}\right) \, \mathbf{a}_{3}$ | = | $- a x_{5} \,\mathbf{\hat{x}}- b \left(y_{5} - \frac{1}{2}\right) \,\mathbf{\hat{y}}+c z_{5} \,\mathbf{\hat{z}}$ | (16j) | H II |
| $\mathbf{B_{17}}$ | = | $\left(y_{5} - z_{5} + \frac{1}{2}\right) \, \mathbf{a}_{1}- \left(x_{5} + z_{5}\right) \, \mathbf{a}_{2}+\left(- x_{5} + y_{5} + \frac{1}{2}\right) \, \mathbf{a}_{3}$ | = | $- a x_{5} \,\mathbf{\hat{x}}+b \left(y_{5} + \frac{1}{2}\right) \,\mathbf{\hat{y}}- c z_{5} \,\mathbf{\hat{z}}$ | (16j) | H II |
| $\mathbf{B_{18}}$ | = | $- \left(y_{5} + z_{5}\right) \, \mathbf{a}_{1}+\left(x_{5} - z_{5}\right) \, \mathbf{a}_{2}+\left(x_{5} - y_{5}\right) \, \mathbf{a}_{3}$ | = | $a x_{5} \,\mathbf{\hat{x}}- b y_{5} \,\mathbf{\hat{y}}- c z_{5} \,\mathbf{\hat{z}}$ | (16j) | H II |
| $\mathbf{B_{19}}$ | = | $- \left(y_{5} + z_{5}\right) \, \mathbf{a}_{1}- \left(x_{5} + z_{5}\right) \, \mathbf{a}_{2}- \left(x_{5} + y_{5}\right) \, \mathbf{a}_{3}$ | = | $- a x_{5} \,\mathbf{\hat{x}}- b y_{5} \,\mathbf{\hat{y}}- c z_{5} \,\mathbf{\hat{z}}$ | (16j) | H II |
| $\mathbf{B_{20}}$ | = | $\left(y_{5} - z_{5} + \frac{1}{2}\right) \, \mathbf{a}_{1}+\left(x_{5} - z_{5}\right) \, \mathbf{a}_{2}+\left(x_{5} + y_{5} + \frac{1}{2}\right) \, \mathbf{a}_{3}$ | = | $a x_{5} \,\mathbf{\hat{x}}+b \left(y_{5} + \frac{1}{2}\right) \,\mathbf{\hat{y}}- c z_{5} \,\mathbf{\hat{z}}$ | (16j) | H II |
| $\mathbf{B_{21}}$ | = | $\left(- y_{5} + z_{5} + \frac{1}{2}\right) \, \mathbf{a}_{1}+\left(x_{5} + z_{5}\right) \, \mathbf{a}_{2}+\left(x_{5} - y_{5} + \frac{1}{2}\right) \, \mathbf{a}_{3}$ | = | $a x_{5} \,\mathbf{\hat{x}}- b \left(y_{5} - \frac{1}{2}\right) \,\mathbf{\hat{y}}+c z_{5} \,\mathbf{\hat{z}}$ | (16j) | H II |
| $\mathbf{B_{22}}$ | = | $\left(y_{5} + z_{5}\right) \, \mathbf{a}_{1}- \left(x_{5} - z_{5}\right) \, \mathbf{a}_{2}- \left(x_{5} - y_{5}\right) \, \mathbf{a}_{3}$ | = | $- a x_{5} \,\mathbf{\hat{x}}+b y_{5} \,\mathbf{\hat{y}}+c z_{5} \,\mathbf{\hat{z}}$ | (16j) | H II |
References
- T. Ivšić, D. W. Bi, and A. Magrez, New refinement of the crystal structure of Zn(NH$_{3}$)Cl$_{2}$ at 100K, Acta Crystallogr. Sect. E 75, 1386–1388 (2019), doi:10.1107/S2056989019011757.
- T. Yamaguchi and O. Lindqvist, The Crystal Structure of Diamminedichlorozinc(II), ZnCl$_{2}$(NH$_{3}$)$_{2}$. A New Refinement., Acta Chem. Scand. 37a, 727–728 (1981), doi:10.3891/acta.chem.scand.35a-0727.
Prototype Generator
aflow --proto=A2B6C2D_oI44_74_i_hj_h_e --params=$a,b/a,c/a,z_{1},y_{2},z_{2},y_{3},z_{3},x_{4},z_{4},x_{5},y_{5},z_{5}$