The Trigonal Crystal System
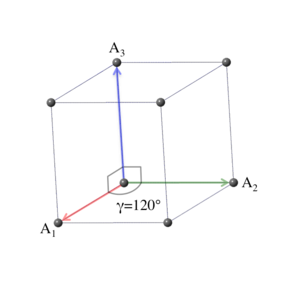
The trigonal crystal system is defined by a three-fold rotation axis, and can be generated from the cubic crystal system by stretching the cube along its diagonal. The symmetry requires the primitive vectors to have the form $a = b$, $\alpha = \beta = \pi/2$, $\gamma = 120^\circ$. We could take $\gamma = 60^\circ$, but in that case the three-fold rotation axis is not obvious from the primitive vectors. The trigonal system is a limiting case of the simple monoclinic Bravais lattice with $\beta = 120^\circ$. It can also be obtained from the base-centered orthorhombic Bravais lattice with $b = \sqrt3 a$. The conventional unit cell is described by the vectors
\[ \begin{array}{ccc} \mathbf{A}_1 & = & \frac{a}{2} \, \mathbf{\hat{x}} - \frac{\sqrt{3}}{2} \, a \, \mathbf{\hat{y}} \nonumber \\ \mathbf{A}_2 & = & \frac{a}{2} \, \mathbf{\hat{x}} + \frac{\sqrt{3}}{2} \, a \, \mathbf{\hat{y}} \nonumber \\ \mathbf{A}_3 & = & c \, \mathbf{\hat{z}}. \end{array} \]
There are two Bravais lattices in the trigonal system.
Lattice 10: Hexagonal

Somewhat confusingly, what might be called the simple trigonal Bravais lattice is known as the hexagonal lattice, as it shares the same primitive vectors,but not point operations, as the hexagonal crystal system. The primitive vectors are identical to those of the conventional cell,
\[ \begin{array}{ccc} \mathbf{a}_1 & = & \frac{a}{2} \, \mathbf{\hat{x}} - \frac{\sqrt{3}}{2} \, a \, \mathbf{\hat{y}} \nonumber \\ \mathbf{a}_2 & = & \frac{a}{2} \, \mathbf{\hat{x}} + \frac{\sqrt{3}}{2} \, a \, \mathbf{\hat{y}} \nonumber \\ \mathbf{a}_3 & = & c \, \mathbf{\hat{z}}. \end{array} \]
The volume of the primitive cell is \[ V = \left(\frac{\sqrt3}{2}\right) \, a^2 \, c. \]
The space groups associated with the (trigonal) hexagonal lattice are:
\[ \begin{array}{lll} 143. ~ \text{P3} & 144. ~ \text{P3$_{1}$} & 145. ~ \text{P3$_{2}$} \\ 147. ~ \text{P$\overline{3}$} & 149. ~ \text{P312} & 150. ~ \text{P321} \\ 151. ~ \text{P3$_{1}$12} & 152. ~ \text{P3$_{1}$21} & 153. ~ \text{P3$_{2}$12} \\ 154. ~ \text{P3$_{2}$21} & 156. ~ \text{P3m1} & 157. ~ \text{P31m} \\ 158. ~ \text{P3c1} & 159. ~ \text{P31c} & 162. ~ \text{P$\overline{3}$1m} \\ 163. ~ \text{P$\overline{3}$1c} & 164. ~ \text{P$\overline{3}$m1} & 165. ~ \text{P$\overline{3}$c1} \\ \end{array} \]
Lattice 11: Rhombohedral

The rhombohedral Bravais lattice has the periodicity of the conventional trigonal cell, with the addition of two translation vectors, $2/3 \mathbf{A}_1 + 1/3 \mathbf{A}_2 + 1/3 \mathbf{A}_3$ and $1/3 \mathbf{A}_1 + 2/3 \mathbf{A}_2 + 2/3 \mathbf{A}_3$. The primitive vectors can be written in the form:
\[ \begin{array}{ccc} \mathbf{a}_1 & = & ~ \frac{a}{2} \, \mathbf{\hat{x}} - \frac{a}{\left(2 \sqrt{3}\right)} \, \mathbf{\hat{y}} + \frac{c}{3} \, \mathbf{\hat{z}} \nonumber \\ \mathbf{a}_2 & = & \frac{a}{\sqrt{3}} \, \mathbf{\hat{y}} + \frac{c}{3} \, \mathbf{\hat{z}} \nonumber \\ \mathbf{a}_3 & = & - \frac{a}{2} \, \mathbf{\hat{x}} - \frac{a}{\left(2 \sqrt{3}\right)} \, \mathbf{\hat{y}} + \frac{c}{3} \, \mathbf{\hat{z}}, \end{array} \]
and the volume of the primitive cell is one-third that of the conventional cell, \[ V = \left(\frac{2}{\sqrt3}\right) \, a^2 \, c. \]
The vectors above are all of identical length, \[ |\mathbf{a}_1| = |\mathbf{a}_2| = |\mathbf{a}_3| = \sqrt{\frac{a^2}{3} + \frac{c^2}{9}} \equiv a', \] or, equivalently, $a = b = c \equiv a'$, where we designate the common length as $a'$ to distinguish it from the length of the first two vectors in the conventional lattice. The vectors also make equal angles with each other:
\[ \alpha = \beta = \gamma = \cos^{-1} \left(\frac{2 c^2 - 3 a^2}{2 \left( c^2 + 3 a^2 \right)}\right). \]
The above equations provide another definition of the rhombohedral lattice. We can show this by writing the primitive vectors in a form that depends only on the common length and separation angle.
\[ \begin{array}{ccc} \mathbf{a}_1 & = & a' \left( \begin{array}{c} \sin\frac{\alpha}{2} ~ \mathbf{\hat{x}} \\ - \left(\frac{1}{\sqrt{3}}\right) \, \sin\frac{\alpha}{2} ~ \mathbf{\hat{y}} \\ + \sqrt{\frac{1}{3}\left(4 \cos^2\frac{\alpha}{2} - 1\right)} ~ \mathbf{\hat{z}} \end{array} \right) \nonumber \\ \mathbf{a}_2 & = & a' \left( \begin{array}{c} \left(2/\sqrt{3}\right) \, \sin\frac{\alpha}{2} ~ \mathbf{\hat{y}} \\ + \sqrt{\frac{1}{3}\left(4 \cos^2\frac{\alpha}{2} - 1\right)} ~ \mathbf{\hat{z}} \end{array} \right) \nonumber \\ \mathbf{a}_3 & = & a' \left( \begin{array}{c} - \sin\frac{\alpha}{2} ~ \mathbf{\hat{x}} \\ - \left(\frac{1}{\sqrt{3}}\right) \, \sin\frac{\alpha}{2} ~ \mathbf{\hat{y}} \\ + \sqrt{\frac{1}{3}\left(4 \cos^2\frac{\alpha}{2} - 1\right)} ~ \mathbf{\hat{z}} \end{array} \right). \end{array} \]
An alternative orientation is given by Setyawan and Curtarolo who only give the primitive vectors in this $(a',\alpha)$ setting. The primitive vectors used for their rhombohedral cell differ from the equations above only by the orientation of the vectors relative to the Cartesian axes. Their choice is simpler for computational purposes, but does not show the relationship between the $(a,c)$ and $(a',\alpha)$ variants.
We can define the rhombohedral lattice in two ways:
as a trigonal lattice with additional translational vectors, or as
a simple
lattice with primitive vectors of equal length
making equal angles with one another. The International
Tables address this ambiguity by listing atomic positions for
the rhombohedral lattice in a hexagonal setting,
where all
coordinates are referenced to the conventional cell, and in
a rhombohedral setting,
where the coordinates are
referenced to rhombohedral lattice. To further confuse matters,
the unit cell's dimensions might be reported in terms of $(a,c)$
or in terms of $(a',\alpha)$. An article might say that there were
N atoms in the rhombohedral cell, or 3N atoms in the conventional
cell. One has to pay attention to the context. In the database, we
will report the lattice parameters of the system by giving $a$ and
$c$, since that is the usual crystallographic practice. However,
we will record atomic positions using the rhombohedral primitive
vectors, since computer calculations work best with the smallest
number of atoms needed to describe the system.
The space groups associated with the rhombohedral lattice are:
\[ \begin{array}{lll} 146. ~ \text{R3} & 148. ~ \text{R$\overline{3}$} & 155. ~ \text{R32} \\ 160. ~ \text{R3m} & 161. ~ \text{R3c} & 166. ~ \text{R$\overline{3}$m} \\ 167. ~ \text{R$\overline{3}$c} & ~ & ~ \\ \end{array} \]