Enantiomorphic space groups
In affine space — i.e., no defined origin — there are only 219 space groups (referred to as the affine space groups). The eleven remaining space groups are mirror images (left‐handed versus right‐handed structures) of one of the other 219 space groups and are equivalent in the affine space. These pairs of space groups are the enantiomorphic pairs, in which two prototypes can be formed as mirror images of a single structure. The eleven pairs of enantiomorphic space groups (Online Dictionary of Crystallography, ITC-A) are:
- $P4_{1}$ (#76) and $P4_{3}$ (#78),
- $P4_{1}22$ (#91) and $P4_{3}22$ (#95),
- $P4_{1}2_{1}2$ (#92) and $P4_{3}2_{1}2$ (#96),
- $P3_{1}$ (#144) and $P3_{2}$ (#145),
- $P3_{1}12$ (#151) and $P3_{2}12$ (#153),
- $P3_{1}21$ (#152) and $P3_{2}21$ (#154),
- $P6_{1}$ (#169) and $P6_{5}$ (#170),
- $P6_{2}$ (#171) and $P6_{4}$ (#172),
- $P6_{1}22$ (#178) and $P6_{5}22$ (#179),
- $P6_{2}22$ (#180) and $P6_{4}22$ (#181), and
- $P4_{1}32$ (#213) and $P4_{3}32$ (#212).
The relationship between the enantiomorphic pairs is exploited in this encyclopedia to generate prototypes for otherwise unrepresented space groups. If we look at space group $P4_{1}$ (#76), we see that it has one Wyckoff position ($4a$), with operations (Bilbao Crystallographic Server):
If we then look at space group $P4_{3}$ (#78), we find it also has one ($4a$) Wyckoff position, with operations
where the only difference is that the 1/4 and 3/4
fractions have swapped positions. We can easily show that space
group #78 is a mirror reflection of #76 in the $z = 0$ plane. To see
this more clearly, consider the Cs3P7
structure (A3B7_tP40_76_3a_7a). This structure was found in space
group #76, but if we reflect all of the coordinates through the $z =
0$ plane, it transforms into a structure in space group #78, as
shown below. 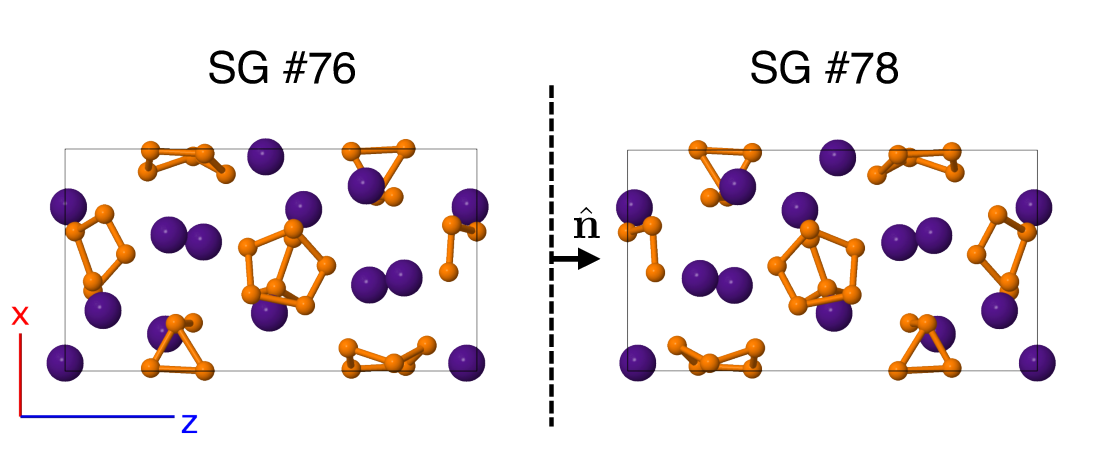 The distance between any pair of atoms is the same
in the $P4_{3}$ structure as it is in the $P4_{1}$ structure, and
the angle between any three atoms is the same in both structures. It
follows that the structures are degenerate, there is no difference
in energy between them, and they should be equally likely to
form. Any structure in space group $P4_{1}$ can be transformed into
$P4_{3}$ by this method. Pairs of space groups which allow these
transformations are said to be enantiomorphic
(Online Dictionary of
Crystallography, ITC-A), or
chiral. In addition, forty-three other space groups allow chiral
crystal structures. The complete set of sixty-five space groups are
known as the Sohncke groups
(Online Dictionary of
Crystallography).
The distance between any pair of atoms is the same
in the $P4_{3}$ structure as it is in the $P4_{1}$ structure, and
the angle between any three atoms is the same in both structures. It
follows that the structures are degenerate, there is no difference
in energy between them, and they should be equally likely to
form. Any structure in space group $P4_{1}$ can be transformed into
$P4_{3}$ by this method. Pairs of space groups which allow these
transformations are said to be enantiomorphic
(Online Dictionary of
Crystallography, ITC-A), or
chiral. In addition, forty-three other space groups allow chiral
crystal structures. The complete set of sixty-five space groups are
known as the Sohncke groups
(Online Dictionary of
Crystallography).