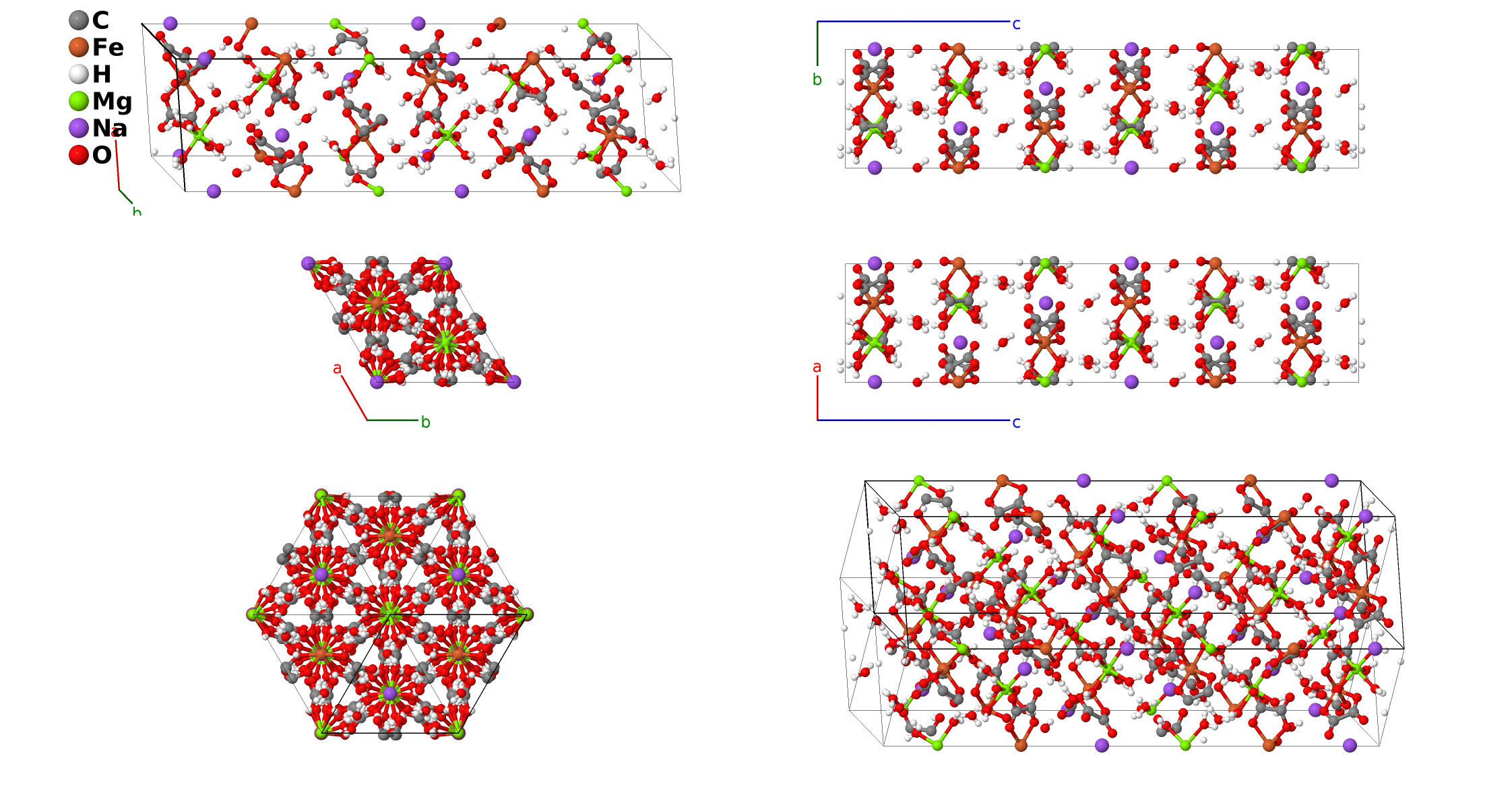
Stepanovite (NaMgFe(C$_{2}$O$_{4}$)$_{3}\cdot$9H$_{2}$O) Structure: A6BC18DEF21_hR96_161_2b_a_6b_a_a_7b-001
| Prototype | C$_{2}$FeH$_{6}$MgNaO$_{7}$ |
| AFLOW prototype label | A6BC18DEF21_hR96_161_2b_a_6b_a_a_7b-001 |
| Mineral name | stepanovite |
| ICSD | 252894 |
| Pearson symbol | hR96 |
| Space group number | 161 |
| Space group symbol | $R3c$ |
| AFLOW prototype command |
aflow --proto=A6BC18DEF21_hR96_161_2b_a_6b_a_a_7b-001
--params=$a, \allowbreak c/a, \allowbreak x_{1}, \allowbreak x_{2}, \allowbreak x_{3}, \allowbreak x_{4}, \allowbreak y_{4}, \allowbreak z_{4}, \allowbreak x_{5}, \allowbreak y_{5}, \allowbreak z_{5}, \allowbreak x_{6}, \allowbreak y_{6}, \allowbreak z_{6}, \allowbreak x_{7}, \allowbreak y_{7}, \allowbreak z_{7}, \allowbreak x_{8}, \allowbreak y_{8}, \allowbreak z_{8}, \allowbreak x_{9}, \allowbreak y_{9}, \allowbreak z_{9}, \allowbreak x_{10}, \allowbreak y_{10}, \allowbreak z_{10}, \allowbreak x_{11}, \allowbreak y_{11}, \allowbreak z_{11}, \allowbreak x_{12}, \allowbreak y_{12}, \allowbreak z_{12}, \allowbreak x_{13}, \allowbreak y_{13}, \allowbreak z_{13}, \allowbreak x_{14}, \allowbreak y_{14}, \allowbreak z_{14}, \allowbreak x_{15}, \allowbreak y_{15}, \allowbreak z_{15}, \allowbreak x_{16}, \allowbreak y_{16}, \allowbreak z_{16}, \allowbreak x_{17}, \allowbreak y_{17}, \allowbreak z_{17}, \allowbreak x_{18}, \allowbreak y_{18}, \allowbreak z_{18}$ |
Other compounds with this structure
NaMgAl(C$_{2}$O$_{4}$)$_{3}\cdot$8H$_{2}$O (zhemchuzhnikovite)
- We use the data for stoichiometric synthetic stepanovite from (Huskć, 2016). Natural stepanovite, as well as zhemchuzhnikovite, contains between 8 and 9 water molecules per formula unit.
- Hexagonal settings of this structure can be obtained with the option
--hex.
\[ \begin{array}{ccc}
\mathbf{a_{1}}&=&\frac{1}{2}a \,\mathbf{\hat{x}}- \frac{\sqrt{3}}{6}a \,\mathbf{\hat{y}}+\frac{1}{3}c \,\mathbf{\hat{z}}\\\mathbf{a_{2}}&=&\frac{1}{\sqrt{3}}a \,\mathbf{\hat{y}}+\frac{1}{3}c \,\mathbf{\hat{z}}\\\mathbf{a_{3}}&=&- \frac{1}{2}a \,\mathbf{\hat{x}}- \frac{\sqrt{3}}{6}a \,\mathbf{\hat{y}}+\frac{1}{3}c \,\mathbf{\hat{z}}
\end{array}\]
Basis vectors
| Lattice coordinates | Cartesian coordinates | Wyckoff position | Atom type | |||
|---|---|---|---|---|---|---|
| $\mathbf{B_{1}}$ | = | $x_{1} \, \mathbf{a}_{1}+x_{1} \, \mathbf{a}_{2}+x_{1} \, \mathbf{a}_{3}$ | = | $c x_{1} \,\mathbf{\hat{z}}$ | (2a) | Fe I |
| $\mathbf{B_{2}}$ | = | $\left(x_{1} + \frac{1}{2}\right) \, \mathbf{a}_{1}+\left(x_{1} + \frac{1}{2}\right) \, \mathbf{a}_{2}+\left(x_{1} + \frac{1}{2}\right) \, \mathbf{a}_{3}$ | = | $c \left(x_{1} + \frac{1}{2}\right) \,\mathbf{\hat{z}}$ | (2a) | Fe I |
| $\mathbf{B_{3}}$ | = | $x_{2} \, \mathbf{a}_{1}+x_{2} \, \mathbf{a}_{2}+x_{2} \, \mathbf{a}_{3}$ | = | $c x_{2} \,\mathbf{\hat{z}}$ | (2a) | Mg I |
| $\mathbf{B_{4}}$ | = | $\left(x_{2} + \frac{1}{2}\right) \, \mathbf{a}_{1}+\left(x_{2} + \frac{1}{2}\right) \, \mathbf{a}_{2}+\left(x_{2} + \frac{1}{2}\right) \, \mathbf{a}_{3}$ | = | $c \left(x_{2} + \frac{1}{2}\right) \,\mathbf{\hat{z}}$ | (2a) | Mg I |
| $\mathbf{B_{5}}$ | = | $x_{3} \, \mathbf{a}_{1}+x_{3} \, \mathbf{a}_{2}+x_{3} \, \mathbf{a}_{3}$ | = | $c x_{3} \,\mathbf{\hat{z}}$ | (2a) | Na I |
| $\mathbf{B_{6}}$ | = | $\left(x_{3} + \frac{1}{2}\right) \, \mathbf{a}_{1}+\left(x_{3} + \frac{1}{2}\right) \, \mathbf{a}_{2}+\left(x_{3} + \frac{1}{2}\right) \, \mathbf{a}_{3}$ | = | $c \left(x_{3} + \frac{1}{2}\right) \,\mathbf{\hat{z}}$ | (2a) | Na I |
| $\mathbf{B_{7}}$ | = | $x_{4} \, \mathbf{a}_{1}+y_{4} \, \mathbf{a}_{2}+z_{4} \, \mathbf{a}_{3}$ | = | $\frac{1}{2}a \left(x_{4} - z_{4}\right) \,\mathbf{\hat{x}}- \frac{\sqrt{3}}{6}a \left(x_{4} - 2 y_{4} + z_{4}\right) \,\mathbf{\hat{y}}+\frac{1}{3}c \left(x_{4} + y_{4} + z_{4}\right) \,\mathbf{\hat{z}}$ | (6b) | C I |
| $\mathbf{B_{8}}$ | = | $z_{4} \, \mathbf{a}_{1}+x_{4} \, \mathbf{a}_{2}+y_{4} \, \mathbf{a}_{3}$ | = | $- \frac{1}{2}a \left(y_{4} - z_{4}\right) \,\mathbf{\hat{x}}+\frac{\sqrt{3}}{6}a \left(2 x_{4} - y_{4} - z_{4}\right) \,\mathbf{\hat{y}}+\frac{1}{3}c \left(x_{4} + y_{4} + z_{4}\right) \,\mathbf{\hat{z}}$ | (6b) | C I |
| $\mathbf{B_{9}}$ | = | $y_{4} \, \mathbf{a}_{1}+z_{4} \, \mathbf{a}_{2}+x_{4} \, \mathbf{a}_{3}$ | = | $- \frac{1}{2}a \left(x_{4} - y_{4}\right) \,\mathbf{\hat{x}}- \frac{\sqrt{3}}{6}a \left(x_{4} + y_{4} - 2 z_{4}\right) \,\mathbf{\hat{y}}+\frac{1}{3}c \left(x_{4} + y_{4} + z_{4}\right) \,\mathbf{\hat{z}}$ | (6b) | C I |
| $\mathbf{B_{10}}$ | = | $\left(z_{4} + \frac{1}{2}\right) \, \mathbf{a}_{1}+\left(y_{4} + \frac{1}{2}\right) \, \mathbf{a}_{2}+\left(x_{4} + \frac{1}{2}\right) \, \mathbf{a}_{3}$ | = | $- \frac{1}{2}a \left(x_{4} - z_{4}\right) \,\mathbf{\hat{x}}- \frac{\sqrt{3}}{6}a \left(x_{4} - 2 y_{4} + z_{4}\right) \,\mathbf{\hat{y}}+\frac{1}{6}c \left(2 x_{4} + 2 y_{4} + 2 z_{4} + 3\right) \,\mathbf{\hat{z}}$ | (6b) | C I |
| $\mathbf{B_{11}}$ | = | $\left(y_{4} + \frac{1}{2}\right) \, \mathbf{a}_{1}+\left(x_{4} + \frac{1}{2}\right) \, \mathbf{a}_{2}+\left(z_{4} + \frac{1}{2}\right) \, \mathbf{a}_{3}$ | = | $\frac{1}{2}a \left(y_{4} - z_{4}\right) \,\mathbf{\hat{x}}+\frac{\sqrt{3}}{6}a \left(2 x_{4} - y_{4} - z_{4}\right) \,\mathbf{\hat{y}}+\frac{1}{6}c \left(2 x_{4} + 2 y_{4} + 2 z_{4} + 3\right) \,\mathbf{\hat{z}}$ | (6b) | C I |
| $\mathbf{B_{12}}$ | = | $\left(x_{4} + \frac{1}{2}\right) \, \mathbf{a}_{1}+\left(z_{4} + \frac{1}{2}\right) \, \mathbf{a}_{2}+\left(y_{4} + \frac{1}{2}\right) \, \mathbf{a}_{3}$ | = | $\frac{1}{2}a \left(x_{4} - y_{4}\right) \,\mathbf{\hat{x}}- \frac{\sqrt{3}}{6}a \left(x_{4} + y_{4} - 2 z_{4}\right) \,\mathbf{\hat{y}}+\frac{1}{6}c \left(2 x_{4} + 2 y_{4} + 2 z_{4} + 3\right) \,\mathbf{\hat{z}}$ | (6b) | C I |
| $\mathbf{B_{13}}$ | = | $x_{5} \, \mathbf{a}_{1}+y_{5} \, \mathbf{a}_{2}+z_{5} \, \mathbf{a}_{3}$ | = | $\frac{1}{2}a \left(x_{5} - z_{5}\right) \,\mathbf{\hat{x}}- \frac{\sqrt{3}}{6}a \left(x_{5} - 2 y_{5} + z_{5}\right) \,\mathbf{\hat{y}}+\frac{1}{3}c \left(x_{5} + y_{5} + z_{5}\right) \,\mathbf{\hat{z}}$ | (6b) | C II |
| $\mathbf{B_{14}}$ | = | $z_{5} \, \mathbf{a}_{1}+x_{5} \, \mathbf{a}_{2}+y_{5} \, \mathbf{a}_{3}$ | = | $- \frac{1}{2}a \left(y_{5} - z_{5}\right) \,\mathbf{\hat{x}}+\frac{\sqrt{3}}{6}a \left(2 x_{5} - y_{5} - z_{5}\right) \,\mathbf{\hat{y}}+\frac{1}{3}c \left(x_{5} + y_{5} + z_{5}\right) \,\mathbf{\hat{z}}$ | (6b) | C II |
| $\mathbf{B_{15}}$ | = | $y_{5} \, \mathbf{a}_{1}+z_{5} \, \mathbf{a}_{2}+x_{5} \, \mathbf{a}_{3}$ | = | $- \frac{1}{2}a \left(x_{5} - y_{5}\right) \,\mathbf{\hat{x}}- \frac{\sqrt{3}}{6}a \left(x_{5} + y_{5} - 2 z_{5}\right) \,\mathbf{\hat{y}}+\frac{1}{3}c \left(x_{5} + y_{5} + z_{5}\right) \,\mathbf{\hat{z}}$ | (6b) | C II |
| $\mathbf{B_{16}}$ | = | $\left(z_{5} + \frac{1}{2}\right) \, \mathbf{a}_{1}+\left(y_{5} + \frac{1}{2}\right) \, \mathbf{a}_{2}+\left(x_{5} + \frac{1}{2}\right) \, \mathbf{a}_{3}$ | = | $- \frac{1}{2}a \left(x_{5} - z_{5}\right) \,\mathbf{\hat{x}}- \frac{\sqrt{3}}{6}a \left(x_{5} - 2 y_{5} + z_{5}\right) \,\mathbf{\hat{y}}+\frac{1}{6}c \left(2 x_{5} + 2 y_{5} + 2 z_{5} + 3\right) \,\mathbf{\hat{z}}$ | (6b) | C II |
| $\mathbf{B_{17}}$ | = | $\left(y_{5} + \frac{1}{2}\right) \, \mathbf{a}_{1}+\left(x_{5} + \frac{1}{2}\right) \, \mathbf{a}_{2}+\left(z_{5} + \frac{1}{2}\right) \, \mathbf{a}_{3}$ | = | $\frac{1}{2}a \left(y_{5} - z_{5}\right) \,\mathbf{\hat{x}}+\frac{\sqrt{3}}{6}a \left(2 x_{5} - y_{5} - z_{5}\right) \,\mathbf{\hat{y}}+\frac{1}{6}c \left(2 x_{5} + 2 y_{5} + 2 z_{5} + 3\right) \,\mathbf{\hat{z}}$ | (6b) | C II |
| $\mathbf{B_{18}}$ | = | $\left(x_{5} + \frac{1}{2}\right) \, \mathbf{a}_{1}+\left(z_{5} + \frac{1}{2}\right) \, \mathbf{a}_{2}+\left(y_{5} + \frac{1}{2}\right) \, \mathbf{a}_{3}$ | = | $\frac{1}{2}a \left(x_{5} - y_{5}\right) \,\mathbf{\hat{x}}- \frac{\sqrt{3}}{6}a \left(x_{5} + y_{5} - 2 z_{5}\right) \,\mathbf{\hat{y}}+\frac{1}{6}c \left(2 x_{5} + 2 y_{5} + 2 z_{5} + 3\right) \,\mathbf{\hat{z}}$ | (6b) | C II |
| $\mathbf{B_{19}}$ | = | $x_{6} \, \mathbf{a}_{1}+y_{6} \, \mathbf{a}_{2}+z_{6} \, \mathbf{a}_{3}$ | = | $\frac{1}{2}a \left(x_{6} - z_{6}\right) \,\mathbf{\hat{x}}- \frac{\sqrt{3}}{6}a \left(x_{6} - 2 y_{6} + z_{6}\right) \,\mathbf{\hat{y}}+\frac{1}{3}c \left(x_{6} + y_{6} + z_{6}\right) \,\mathbf{\hat{z}}$ | (6b) | H I |
| $\mathbf{B_{20}}$ | = | $z_{6} \, \mathbf{a}_{1}+x_{6} \, \mathbf{a}_{2}+y_{6} \, \mathbf{a}_{3}$ | = | $- \frac{1}{2}a \left(y_{6} - z_{6}\right) \,\mathbf{\hat{x}}+\frac{\sqrt{3}}{6}a \left(2 x_{6} - y_{6} - z_{6}\right) \,\mathbf{\hat{y}}+\frac{1}{3}c \left(x_{6} + y_{6} + z_{6}\right) \,\mathbf{\hat{z}}$ | (6b) | H I |
| $\mathbf{B_{21}}$ | = | $y_{6} \, \mathbf{a}_{1}+z_{6} \, \mathbf{a}_{2}+x_{6} \, \mathbf{a}_{3}$ | = | $- \frac{1}{2}a \left(x_{6} - y_{6}\right) \,\mathbf{\hat{x}}- \frac{\sqrt{3}}{6}a \left(x_{6} + y_{6} - 2 z_{6}\right) \,\mathbf{\hat{y}}+\frac{1}{3}c \left(x_{6} + y_{6} + z_{6}\right) \,\mathbf{\hat{z}}$ | (6b) | H I |
| $\mathbf{B_{22}}$ | = | $\left(z_{6} + \frac{1}{2}\right) \, \mathbf{a}_{1}+\left(y_{6} + \frac{1}{2}\right) \, \mathbf{a}_{2}+\left(x_{6} + \frac{1}{2}\right) \, \mathbf{a}_{3}$ | = | $- \frac{1}{2}a \left(x_{6} - z_{6}\right) \,\mathbf{\hat{x}}- \frac{\sqrt{3}}{6}a \left(x_{6} - 2 y_{6} + z_{6}\right) \,\mathbf{\hat{y}}+\frac{1}{6}c \left(2 x_{6} + 2 y_{6} + 2 z_{6} + 3\right) \,\mathbf{\hat{z}}$ | (6b) | H I |
| $\mathbf{B_{23}}$ | = | $\left(y_{6} + \frac{1}{2}\right) \, \mathbf{a}_{1}+\left(x_{6} + \frac{1}{2}\right) \, \mathbf{a}_{2}+\left(z_{6} + \frac{1}{2}\right) \, \mathbf{a}_{3}$ | = | $\frac{1}{2}a \left(y_{6} - z_{6}\right) \,\mathbf{\hat{x}}+\frac{\sqrt{3}}{6}a \left(2 x_{6} - y_{6} - z_{6}\right) \,\mathbf{\hat{y}}+\frac{1}{6}c \left(2 x_{6} + 2 y_{6} + 2 z_{6} + 3\right) \,\mathbf{\hat{z}}$ | (6b) | H I |
| $\mathbf{B_{24}}$ | = | $\left(x_{6} + \frac{1}{2}\right) \, \mathbf{a}_{1}+\left(z_{6} + \frac{1}{2}\right) \, \mathbf{a}_{2}+\left(y_{6} + \frac{1}{2}\right) \, \mathbf{a}_{3}$ | = | $\frac{1}{2}a \left(x_{6} - y_{6}\right) \,\mathbf{\hat{x}}- \frac{\sqrt{3}}{6}a \left(x_{6} + y_{6} - 2 z_{6}\right) \,\mathbf{\hat{y}}+\frac{1}{6}c \left(2 x_{6} + 2 y_{6} + 2 z_{6} + 3\right) \,\mathbf{\hat{z}}$ | (6b) | H I |
| $\mathbf{B_{25}}$ | = | $x_{7} \, \mathbf{a}_{1}+y_{7} \, \mathbf{a}_{2}+z_{7} \, \mathbf{a}_{3}$ | = | $\frac{1}{2}a \left(x_{7} - z_{7}\right) \,\mathbf{\hat{x}}- \frac{\sqrt{3}}{6}a \left(x_{7} - 2 y_{7} + z_{7}\right) \,\mathbf{\hat{y}}+\frac{1}{3}c \left(x_{7} + y_{7} + z_{7}\right) \,\mathbf{\hat{z}}$ | (6b) | H II |
| $\mathbf{B_{26}}$ | = | $z_{7} \, \mathbf{a}_{1}+x_{7} \, \mathbf{a}_{2}+y_{7} \, \mathbf{a}_{3}$ | = | $- \frac{1}{2}a \left(y_{7} - z_{7}\right) \,\mathbf{\hat{x}}+\frac{\sqrt{3}}{6}a \left(2 x_{7} - y_{7} - z_{7}\right) \,\mathbf{\hat{y}}+\frac{1}{3}c \left(x_{7} + y_{7} + z_{7}\right) \,\mathbf{\hat{z}}$ | (6b) | H II |
| $\mathbf{B_{27}}$ | = | $y_{7} \, \mathbf{a}_{1}+z_{7} \, \mathbf{a}_{2}+x_{7} \, \mathbf{a}_{3}$ | = | $- \frac{1}{2}a \left(x_{7} - y_{7}\right) \,\mathbf{\hat{x}}- \frac{\sqrt{3}}{6}a \left(x_{7} + y_{7} - 2 z_{7}\right) \,\mathbf{\hat{y}}+\frac{1}{3}c \left(x_{7} + y_{7} + z_{7}\right) \,\mathbf{\hat{z}}$ | (6b) | H II |
| $\mathbf{B_{28}}$ | = | $\left(z_{7} + \frac{1}{2}\right) \, \mathbf{a}_{1}+\left(y_{7} + \frac{1}{2}\right) \, \mathbf{a}_{2}+\left(x_{7} + \frac{1}{2}\right) \, \mathbf{a}_{3}$ | = | $- \frac{1}{2}a \left(x_{7} - z_{7}\right) \,\mathbf{\hat{x}}- \frac{\sqrt{3}}{6}a \left(x_{7} - 2 y_{7} + z_{7}\right) \,\mathbf{\hat{y}}+\frac{1}{6}c \left(2 x_{7} + 2 y_{7} + 2 z_{7} + 3\right) \,\mathbf{\hat{z}}$ | (6b) | H II |
| $\mathbf{B_{29}}$ | = | $\left(y_{7} + \frac{1}{2}\right) \, \mathbf{a}_{1}+\left(x_{7} + \frac{1}{2}\right) \, \mathbf{a}_{2}+\left(z_{7} + \frac{1}{2}\right) \, \mathbf{a}_{3}$ | = | $\frac{1}{2}a \left(y_{7} - z_{7}\right) \,\mathbf{\hat{x}}+\frac{\sqrt{3}}{6}a \left(2 x_{7} - y_{7} - z_{7}\right) \,\mathbf{\hat{y}}+\frac{1}{6}c \left(2 x_{7} + 2 y_{7} + 2 z_{7} + 3\right) \,\mathbf{\hat{z}}$ | (6b) | H II |
| $\mathbf{B_{30}}$ | = | $\left(x_{7} + \frac{1}{2}\right) \, \mathbf{a}_{1}+\left(z_{7} + \frac{1}{2}\right) \, \mathbf{a}_{2}+\left(y_{7} + \frac{1}{2}\right) \, \mathbf{a}_{3}$ | = | $\frac{1}{2}a \left(x_{7} - y_{7}\right) \,\mathbf{\hat{x}}- \frac{\sqrt{3}}{6}a \left(x_{7} + y_{7} - 2 z_{7}\right) \,\mathbf{\hat{y}}+\frac{1}{6}c \left(2 x_{7} + 2 y_{7} + 2 z_{7} + 3\right) \,\mathbf{\hat{z}}$ | (6b) | H II |
| $\mathbf{B_{31}}$ | = | $x_{8} \, \mathbf{a}_{1}+y_{8} \, \mathbf{a}_{2}+z_{8} \, \mathbf{a}_{3}$ | = | $\frac{1}{2}a \left(x_{8} - z_{8}\right) \,\mathbf{\hat{x}}- \frac{\sqrt{3}}{6}a \left(x_{8} - 2 y_{8} + z_{8}\right) \,\mathbf{\hat{y}}+\frac{1}{3}c \left(x_{8} + y_{8} + z_{8}\right) \,\mathbf{\hat{z}}$ | (6b) | H III |
| $\mathbf{B_{32}}$ | = | $z_{8} \, \mathbf{a}_{1}+x_{8} \, \mathbf{a}_{2}+y_{8} \, \mathbf{a}_{3}$ | = | $- \frac{1}{2}a \left(y_{8} - z_{8}\right) \,\mathbf{\hat{x}}+\frac{\sqrt{3}}{6}a \left(2 x_{8} - y_{8} - z_{8}\right) \,\mathbf{\hat{y}}+\frac{1}{3}c \left(x_{8} + y_{8} + z_{8}\right) \,\mathbf{\hat{z}}$ | (6b) | H III |
| $\mathbf{B_{33}}$ | = | $y_{8} \, \mathbf{a}_{1}+z_{8} \, \mathbf{a}_{2}+x_{8} \, \mathbf{a}_{3}$ | = | $- \frac{1}{2}a \left(x_{8} - y_{8}\right) \,\mathbf{\hat{x}}- \frac{\sqrt{3}}{6}a \left(x_{8} + y_{8} - 2 z_{8}\right) \,\mathbf{\hat{y}}+\frac{1}{3}c \left(x_{8} + y_{8} + z_{8}\right) \,\mathbf{\hat{z}}$ | (6b) | H III |
| $\mathbf{B_{34}}$ | = | $\left(z_{8} + \frac{1}{2}\right) \, \mathbf{a}_{1}+\left(y_{8} + \frac{1}{2}\right) \, \mathbf{a}_{2}+\left(x_{8} + \frac{1}{2}\right) \, \mathbf{a}_{3}$ | = | $- \frac{1}{2}a \left(x_{8} - z_{8}\right) \,\mathbf{\hat{x}}- \frac{\sqrt{3}}{6}a \left(x_{8} - 2 y_{8} + z_{8}\right) \,\mathbf{\hat{y}}+\frac{1}{6}c \left(2 x_{8} + 2 y_{8} + 2 z_{8} + 3\right) \,\mathbf{\hat{z}}$ | (6b) | H III |
| $\mathbf{B_{35}}$ | = | $\left(y_{8} + \frac{1}{2}\right) \, \mathbf{a}_{1}+\left(x_{8} + \frac{1}{2}\right) \, \mathbf{a}_{2}+\left(z_{8} + \frac{1}{2}\right) \, \mathbf{a}_{3}$ | = | $\frac{1}{2}a \left(y_{8} - z_{8}\right) \,\mathbf{\hat{x}}+\frac{\sqrt{3}}{6}a \left(2 x_{8} - y_{8} - z_{8}\right) \,\mathbf{\hat{y}}+\frac{1}{6}c \left(2 x_{8} + 2 y_{8} + 2 z_{8} + 3\right) \,\mathbf{\hat{z}}$ | (6b) | H III |
| $\mathbf{B_{36}}$ | = | $\left(x_{8} + \frac{1}{2}\right) \, \mathbf{a}_{1}+\left(z_{8} + \frac{1}{2}\right) \, \mathbf{a}_{2}+\left(y_{8} + \frac{1}{2}\right) \, \mathbf{a}_{3}$ | = | $\frac{1}{2}a \left(x_{8} - y_{8}\right) \,\mathbf{\hat{x}}- \frac{\sqrt{3}}{6}a \left(x_{8} + y_{8} - 2 z_{8}\right) \,\mathbf{\hat{y}}+\frac{1}{6}c \left(2 x_{8} + 2 y_{8} + 2 z_{8} + 3\right) \,\mathbf{\hat{z}}$ | (6b) | H III |
| $\mathbf{B_{37}}$ | = | $x_{9} \, \mathbf{a}_{1}+y_{9} \, \mathbf{a}_{2}+z_{9} \, \mathbf{a}_{3}$ | = | $\frac{1}{2}a \left(x_{9} - z_{9}\right) \,\mathbf{\hat{x}}- \frac{\sqrt{3}}{6}a \left(x_{9} - 2 y_{9} + z_{9}\right) \,\mathbf{\hat{y}}+\frac{1}{3}c \left(x_{9} + y_{9} + z_{9}\right) \,\mathbf{\hat{z}}$ | (6b) | H IV |
| $\mathbf{B_{38}}$ | = | $z_{9} \, \mathbf{a}_{1}+x_{9} \, \mathbf{a}_{2}+y_{9} \, \mathbf{a}_{3}$ | = | $- \frac{1}{2}a \left(y_{9} - z_{9}\right) \,\mathbf{\hat{x}}+\frac{\sqrt{3}}{6}a \left(2 x_{9} - y_{9} - z_{9}\right) \,\mathbf{\hat{y}}+\frac{1}{3}c \left(x_{9} + y_{9} + z_{9}\right) \,\mathbf{\hat{z}}$ | (6b) | H IV |
| $\mathbf{B_{39}}$ | = | $y_{9} \, \mathbf{a}_{1}+z_{9} \, \mathbf{a}_{2}+x_{9} \, \mathbf{a}_{3}$ | = | $- \frac{1}{2}a \left(x_{9} - y_{9}\right) \,\mathbf{\hat{x}}- \frac{\sqrt{3}}{6}a \left(x_{9} + y_{9} - 2 z_{9}\right) \,\mathbf{\hat{y}}+\frac{1}{3}c \left(x_{9} + y_{9} + z_{9}\right) \,\mathbf{\hat{z}}$ | (6b) | H IV |
| $\mathbf{B_{40}}$ | = | $\left(z_{9} + \frac{1}{2}\right) \, \mathbf{a}_{1}+\left(y_{9} + \frac{1}{2}\right) \, \mathbf{a}_{2}+\left(x_{9} + \frac{1}{2}\right) \, \mathbf{a}_{3}$ | = | $- \frac{1}{2}a \left(x_{9} - z_{9}\right) \,\mathbf{\hat{x}}- \frac{\sqrt{3}}{6}a \left(x_{9} - 2 y_{9} + z_{9}\right) \,\mathbf{\hat{y}}+\frac{1}{6}c \left(2 x_{9} + 2 y_{9} + 2 z_{9} + 3\right) \,\mathbf{\hat{z}}$ | (6b) | H IV |
| $\mathbf{B_{41}}$ | = | $\left(y_{9} + \frac{1}{2}\right) \, \mathbf{a}_{1}+\left(x_{9} + \frac{1}{2}\right) \, \mathbf{a}_{2}+\left(z_{9} + \frac{1}{2}\right) \, \mathbf{a}_{3}$ | = | $\frac{1}{2}a \left(y_{9} - z_{9}\right) \,\mathbf{\hat{x}}+\frac{\sqrt{3}}{6}a \left(2 x_{9} - y_{9} - z_{9}\right) \,\mathbf{\hat{y}}+\frac{1}{6}c \left(2 x_{9} + 2 y_{9} + 2 z_{9} + 3\right) \,\mathbf{\hat{z}}$ | (6b) | H IV |
| $\mathbf{B_{42}}$ | = | $\left(x_{9} + \frac{1}{2}\right) \, \mathbf{a}_{1}+\left(z_{9} + \frac{1}{2}\right) \, \mathbf{a}_{2}+\left(y_{9} + \frac{1}{2}\right) \, \mathbf{a}_{3}$ | = | $\frac{1}{2}a \left(x_{9} - y_{9}\right) \,\mathbf{\hat{x}}- \frac{\sqrt{3}}{6}a \left(x_{9} + y_{9} - 2 z_{9}\right) \,\mathbf{\hat{y}}+\frac{1}{6}c \left(2 x_{9} + 2 y_{9} + 2 z_{9} + 3\right) \,\mathbf{\hat{z}}$ | (6b) | H IV |
| $\mathbf{B_{43}}$ | = | $x_{10} \, \mathbf{a}_{1}+y_{10} \, \mathbf{a}_{2}+z_{10} \, \mathbf{a}_{3}$ | = | $\frac{1}{2}a \left(x_{10} - z_{10}\right) \,\mathbf{\hat{x}}- \frac{\sqrt{3}}{6}a \left(x_{10} - 2 y_{10} + z_{10}\right) \,\mathbf{\hat{y}}+\frac{1}{3}c \left(x_{10} + y_{10} + z_{10}\right) \,\mathbf{\hat{z}}$ | (6b) | H V |
| $\mathbf{B_{44}}$ | = | $z_{10} \, \mathbf{a}_{1}+x_{10} \, \mathbf{a}_{2}+y_{10} \, \mathbf{a}_{3}$ | = | $- \frac{1}{2}a \left(y_{10} - z_{10}\right) \,\mathbf{\hat{x}}+\frac{\sqrt{3}}{6}a \left(2 x_{10} - y_{10} - z_{10}\right) \,\mathbf{\hat{y}}+\frac{1}{3}c \left(x_{10} + y_{10} + z_{10}\right) \,\mathbf{\hat{z}}$ | (6b) | H V |
| $\mathbf{B_{45}}$ | = | $y_{10} \, \mathbf{a}_{1}+z_{10} \, \mathbf{a}_{2}+x_{10} \, \mathbf{a}_{3}$ | = | $- \frac{1}{2}a \left(x_{10} - y_{10}\right) \,\mathbf{\hat{x}}- \frac{\sqrt{3}}{6}a \left(x_{10} + y_{10} - 2 z_{10}\right) \,\mathbf{\hat{y}}+\frac{1}{3}c \left(x_{10} + y_{10} + z_{10}\right) \,\mathbf{\hat{z}}$ | (6b) | H V |
| $\mathbf{B_{46}}$ | = | $\left(z_{10} + \frac{1}{2}\right) \, \mathbf{a}_{1}+\left(y_{10} + \frac{1}{2}\right) \, \mathbf{a}_{2}+\left(x_{10} + \frac{1}{2}\right) \, \mathbf{a}_{3}$ | = | $- \frac{1}{2}a \left(x_{10} - z_{10}\right) \,\mathbf{\hat{x}}- \frac{\sqrt{3}}{6}a \left(x_{10} - 2 y_{10} + z_{10}\right) \,\mathbf{\hat{y}}+\frac{1}{6}c \left(2 x_{10} + 2 y_{10} + 2 z_{10} + 3\right) \,\mathbf{\hat{z}}$ | (6b) | H V |
| $\mathbf{B_{47}}$ | = | $\left(y_{10} + \frac{1}{2}\right) \, \mathbf{a}_{1}+\left(x_{10} + \frac{1}{2}\right) \, \mathbf{a}_{2}+\left(z_{10} + \frac{1}{2}\right) \, \mathbf{a}_{3}$ | = | $\frac{1}{2}a \left(y_{10} - z_{10}\right) \,\mathbf{\hat{x}}+\frac{\sqrt{3}}{6}a \left(2 x_{10} - y_{10} - z_{10}\right) \,\mathbf{\hat{y}}+\frac{1}{6}c \left(2 x_{10} + 2 y_{10} + 2 z_{10} + 3\right) \,\mathbf{\hat{z}}$ | (6b) | H V |
| $\mathbf{B_{48}}$ | = | $\left(x_{10} + \frac{1}{2}\right) \, \mathbf{a}_{1}+\left(z_{10} + \frac{1}{2}\right) \, \mathbf{a}_{2}+\left(y_{10} + \frac{1}{2}\right) \, \mathbf{a}_{3}$ | = | $\frac{1}{2}a \left(x_{10} - y_{10}\right) \,\mathbf{\hat{x}}- \frac{\sqrt{3}}{6}a \left(x_{10} + y_{10} - 2 z_{10}\right) \,\mathbf{\hat{y}}+\frac{1}{6}c \left(2 x_{10} + 2 y_{10} + 2 z_{10} + 3\right) \,\mathbf{\hat{z}}$ | (6b) | H V |
| $\mathbf{B_{49}}$ | = | $x_{11} \, \mathbf{a}_{1}+y_{11} \, \mathbf{a}_{2}+z_{11} \, \mathbf{a}_{3}$ | = | $\frac{1}{2}a \left(x_{11} - z_{11}\right) \,\mathbf{\hat{x}}- \frac{\sqrt{3}}{6}a \left(x_{11} - 2 y_{11} + z_{11}\right) \,\mathbf{\hat{y}}+\frac{1}{3}c \left(x_{11} + y_{11} + z_{11}\right) \,\mathbf{\hat{z}}$ | (6b) | H VI |
| $\mathbf{B_{50}}$ | = | $z_{11} \, \mathbf{a}_{1}+x_{11} \, \mathbf{a}_{2}+y_{11} \, \mathbf{a}_{3}$ | = | $- \frac{1}{2}a \left(y_{11} - z_{11}\right) \,\mathbf{\hat{x}}+\frac{\sqrt{3}}{6}a \left(2 x_{11} - y_{11} - z_{11}\right) \,\mathbf{\hat{y}}+\frac{1}{3}c \left(x_{11} + y_{11} + z_{11}\right) \,\mathbf{\hat{z}}$ | (6b) | H VI |
| $\mathbf{B_{51}}$ | = | $y_{11} \, \mathbf{a}_{1}+z_{11} \, \mathbf{a}_{2}+x_{11} \, \mathbf{a}_{3}$ | = | $- \frac{1}{2}a \left(x_{11} - y_{11}\right) \,\mathbf{\hat{x}}- \frac{\sqrt{3}}{6}a \left(x_{11} + y_{11} - 2 z_{11}\right) \,\mathbf{\hat{y}}+\frac{1}{3}c \left(x_{11} + y_{11} + z_{11}\right) \,\mathbf{\hat{z}}$ | (6b) | H VI |
| $\mathbf{B_{52}}$ | = | $\left(z_{11} + \frac{1}{2}\right) \, \mathbf{a}_{1}+\left(y_{11} + \frac{1}{2}\right) \, \mathbf{a}_{2}+\left(x_{11} + \frac{1}{2}\right) \, \mathbf{a}_{3}$ | = | $- \frac{1}{2}a \left(x_{11} - z_{11}\right) \,\mathbf{\hat{x}}- \frac{\sqrt{3}}{6}a \left(x_{11} - 2 y_{11} + z_{11}\right) \,\mathbf{\hat{y}}+\frac{1}{6}c \left(2 x_{11} + 2 y_{11} + 2 z_{11} + 3\right) \,\mathbf{\hat{z}}$ | (6b) | H VI |
| $\mathbf{B_{53}}$ | = | $\left(y_{11} + \frac{1}{2}\right) \, \mathbf{a}_{1}+\left(x_{11} + \frac{1}{2}\right) \, \mathbf{a}_{2}+\left(z_{11} + \frac{1}{2}\right) \, \mathbf{a}_{3}$ | = | $\frac{1}{2}a \left(y_{11} - z_{11}\right) \,\mathbf{\hat{x}}+\frac{\sqrt{3}}{6}a \left(2 x_{11} - y_{11} - z_{11}\right) \,\mathbf{\hat{y}}+\frac{1}{6}c \left(2 x_{11} + 2 y_{11} + 2 z_{11} + 3\right) \,\mathbf{\hat{z}}$ | (6b) | H VI |
| $\mathbf{B_{54}}$ | = | $\left(x_{11} + \frac{1}{2}\right) \, \mathbf{a}_{1}+\left(z_{11} + \frac{1}{2}\right) \, \mathbf{a}_{2}+\left(y_{11} + \frac{1}{2}\right) \, \mathbf{a}_{3}$ | = | $\frac{1}{2}a \left(x_{11} - y_{11}\right) \,\mathbf{\hat{x}}- \frac{\sqrt{3}}{6}a \left(x_{11} + y_{11} - 2 z_{11}\right) \,\mathbf{\hat{y}}+\frac{1}{6}c \left(2 x_{11} + 2 y_{11} + 2 z_{11} + 3\right) \,\mathbf{\hat{z}}$ | (6b) | H VI |
| $\mathbf{B_{55}}$ | = | $x_{12} \, \mathbf{a}_{1}+y_{12} \, \mathbf{a}_{2}+z_{12} \, \mathbf{a}_{3}$ | = | $\frac{1}{2}a \left(x_{12} - z_{12}\right) \,\mathbf{\hat{x}}- \frac{\sqrt{3}}{6}a \left(x_{12} - 2 y_{12} + z_{12}\right) \,\mathbf{\hat{y}}+\frac{1}{3}c \left(x_{12} + y_{12} + z_{12}\right) \,\mathbf{\hat{z}}$ | (6b) | O I |
| $\mathbf{B_{56}}$ | = | $z_{12} \, \mathbf{a}_{1}+x_{12} \, \mathbf{a}_{2}+y_{12} \, \mathbf{a}_{3}$ | = | $- \frac{1}{2}a \left(y_{12} - z_{12}\right) \,\mathbf{\hat{x}}+\frac{\sqrt{3}}{6}a \left(2 x_{12} - y_{12} - z_{12}\right) \,\mathbf{\hat{y}}+\frac{1}{3}c \left(x_{12} + y_{12} + z_{12}\right) \,\mathbf{\hat{z}}$ | (6b) | O I |
| $\mathbf{B_{57}}$ | = | $y_{12} \, \mathbf{a}_{1}+z_{12} \, \mathbf{a}_{2}+x_{12} \, \mathbf{a}_{3}$ | = | $- \frac{1}{2}a \left(x_{12} - y_{12}\right) \,\mathbf{\hat{x}}- \frac{\sqrt{3}}{6}a \left(x_{12} + y_{12} - 2 z_{12}\right) \,\mathbf{\hat{y}}+\frac{1}{3}c \left(x_{12} + y_{12} + z_{12}\right) \,\mathbf{\hat{z}}$ | (6b) | O I |
| $\mathbf{B_{58}}$ | = | $\left(z_{12} + \frac{1}{2}\right) \, \mathbf{a}_{1}+\left(y_{12} + \frac{1}{2}\right) \, \mathbf{a}_{2}+\left(x_{12} + \frac{1}{2}\right) \, \mathbf{a}_{3}$ | = | $- \frac{1}{2}a \left(x_{12} - z_{12}\right) \,\mathbf{\hat{x}}- \frac{\sqrt{3}}{6}a \left(x_{12} - 2 y_{12} + z_{12}\right) \,\mathbf{\hat{y}}+\frac{1}{6}c \left(2 x_{12} + 2 y_{12} + 2 z_{12} + 3\right) \,\mathbf{\hat{z}}$ | (6b) | O I |
| $\mathbf{B_{59}}$ | = | $\left(y_{12} + \frac{1}{2}\right) \, \mathbf{a}_{1}+\left(x_{12} + \frac{1}{2}\right) \, \mathbf{a}_{2}+\left(z_{12} + \frac{1}{2}\right) \, \mathbf{a}_{3}$ | = | $\frac{1}{2}a \left(y_{12} - z_{12}\right) \,\mathbf{\hat{x}}+\frac{\sqrt{3}}{6}a \left(2 x_{12} - y_{12} - z_{12}\right) \,\mathbf{\hat{y}}+\frac{1}{6}c \left(2 x_{12} + 2 y_{12} + 2 z_{12} + 3\right) \,\mathbf{\hat{z}}$ | (6b) | O I |
| $\mathbf{B_{60}}$ | = | $\left(x_{12} + \frac{1}{2}\right) \, \mathbf{a}_{1}+\left(z_{12} + \frac{1}{2}\right) \, \mathbf{a}_{2}+\left(y_{12} + \frac{1}{2}\right) \, \mathbf{a}_{3}$ | = | $\frac{1}{2}a \left(x_{12} - y_{12}\right) \,\mathbf{\hat{x}}- \frac{\sqrt{3}}{6}a \left(x_{12} + y_{12} - 2 z_{12}\right) \,\mathbf{\hat{y}}+\frac{1}{6}c \left(2 x_{12} + 2 y_{12} + 2 z_{12} + 3\right) \,\mathbf{\hat{z}}$ | (6b) | O I |
| $\mathbf{B_{61}}$ | = | $x_{13} \, \mathbf{a}_{1}+y_{13} \, \mathbf{a}_{2}+z_{13} \, \mathbf{a}_{3}$ | = | $\frac{1}{2}a \left(x_{13} - z_{13}\right) \,\mathbf{\hat{x}}- \frac{\sqrt{3}}{6}a \left(x_{13} - 2 y_{13} + z_{13}\right) \,\mathbf{\hat{y}}+\frac{1}{3}c \left(x_{13} + y_{13} + z_{13}\right) \,\mathbf{\hat{z}}$ | (6b) | O II |
| $\mathbf{B_{62}}$ | = | $z_{13} \, \mathbf{a}_{1}+x_{13} \, \mathbf{a}_{2}+y_{13} \, \mathbf{a}_{3}$ | = | $- \frac{1}{2}a \left(y_{13} - z_{13}\right) \,\mathbf{\hat{x}}+\frac{\sqrt{3}}{6}a \left(2 x_{13} - y_{13} - z_{13}\right) \,\mathbf{\hat{y}}+\frac{1}{3}c \left(x_{13} + y_{13} + z_{13}\right) \,\mathbf{\hat{z}}$ | (6b) | O II |
| $\mathbf{B_{63}}$ | = | $y_{13} \, \mathbf{a}_{1}+z_{13} \, \mathbf{a}_{2}+x_{13} \, \mathbf{a}_{3}$ | = | $- \frac{1}{2}a \left(x_{13} - y_{13}\right) \,\mathbf{\hat{x}}- \frac{\sqrt{3}}{6}a \left(x_{13} + y_{13} - 2 z_{13}\right) \,\mathbf{\hat{y}}+\frac{1}{3}c \left(x_{13} + y_{13} + z_{13}\right) \,\mathbf{\hat{z}}$ | (6b) | O II |
| $\mathbf{B_{64}}$ | = | $\left(z_{13} + \frac{1}{2}\right) \, \mathbf{a}_{1}+\left(y_{13} + \frac{1}{2}\right) \, \mathbf{a}_{2}+\left(x_{13} + \frac{1}{2}\right) \, \mathbf{a}_{3}$ | = | $- \frac{1}{2}a \left(x_{13} - z_{13}\right) \,\mathbf{\hat{x}}- \frac{\sqrt{3}}{6}a \left(x_{13} - 2 y_{13} + z_{13}\right) \,\mathbf{\hat{y}}+\frac{1}{6}c \left(2 x_{13} + 2 y_{13} + 2 z_{13} + 3\right) \,\mathbf{\hat{z}}$ | (6b) | O II |
| $\mathbf{B_{65}}$ | = | $\left(y_{13} + \frac{1}{2}\right) \, \mathbf{a}_{1}+\left(x_{13} + \frac{1}{2}\right) \, \mathbf{a}_{2}+\left(z_{13} + \frac{1}{2}\right) \, \mathbf{a}_{3}$ | = | $\frac{1}{2}a \left(y_{13} - z_{13}\right) \,\mathbf{\hat{x}}+\frac{\sqrt{3}}{6}a \left(2 x_{13} - y_{13} - z_{13}\right) \,\mathbf{\hat{y}}+\frac{1}{6}c \left(2 x_{13} + 2 y_{13} + 2 z_{13} + 3\right) \,\mathbf{\hat{z}}$ | (6b) | O II |
| $\mathbf{B_{66}}$ | = | $\left(x_{13} + \frac{1}{2}\right) \, \mathbf{a}_{1}+\left(z_{13} + \frac{1}{2}\right) \, \mathbf{a}_{2}+\left(y_{13} + \frac{1}{2}\right) \, \mathbf{a}_{3}$ | = | $\frac{1}{2}a \left(x_{13} - y_{13}\right) \,\mathbf{\hat{x}}- \frac{\sqrt{3}}{6}a \left(x_{13} + y_{13} - 2 z_{13}\right) \,\mathbf{\hat{y}}+\frac{1}{6}c \left(2 x_{13} + 2 y_{13} + 2 z_{13} + 3\right) \,\mathbf{\hat{z}}$ | (6b) | O II |
| $\mathbf{B_{67}}$ | = | $x_{14} \, \mathbf{a}_{1}+y_{14} \, \mathbf{a}_{2}+z_{14} \, \mathbf{a}_{3}$ | = | $\frac{1}{2}a \left(x_{14} - z_{14}\right) \,\mathbf{\hat{x}}- \frac{\sqrt{3}}{6}a \left(x_{14} - 2 y_{14} + z_{14}\right) \,\mathbf{\hat{y}}+\frac{1}{3}c \left(x_{14} + y_{14} + z_{14}\right) \,\mathbf{\hat{z}}$ | (6b) | O III |
| $\mathbf{B_{68}}$ | = | $z_{14} \, \mathbf{a}_{1}+x_{14} \, \mathbf{a}_{2}+y_{14} \, \mathbf{a}_{3}$ | = | $- \frac{1}{2}a \left(y_{14} - z_{14}\right) \,\mathbf{\hat{x}}+\frac{\sqrt{3}}{6}a \left(2 x_{14} - y_{14} - z_{14}\right) \,\mathbf{\hat{y}}+\frac{1}{3}c \left(x_{14} + y_{14} + z_{14}\right) \,\mathbf{\hat{z}}$ | (6b) | O III |
| $\mathbf{B_{69}}$ | = | $y_{14} \, \mathbf{a}_{1}+z_{14} \, \mathbf{a}_{2}+x_{14} \, \mathbf{a}_{3}$ | = | $- \frac{1}{2}a \left(x_{14} - y_{14}\right) \,\mathbf{\hat{x}}- \frac{\sqrt{3}}{6}a \left(x_{14} + y_{14} - 2 z_{14}\right) \,\mathbf{\hat{y}}+\frac{1}{3}c \left(x_{14} + y_{14} + z_{14}\right) \,\mathbf{\hat{z}}$ | (6b) | O III |
| $\mathbf{B_{70}}$ | = | $\left(z_{14} + \frac{1}{2}\right) \, \mathbf{a}_{1}+\left(y_{14} + \frac{1}{2}\right) \, \mathbf{a}_{2}+\left(x_{14} + \frac{1}{2}\right) \, \mathbf{a}_{3}$ | = | $- \frac{1}{2}a \left(x_{14} - z_{14}\right) \,\mathbf{\hat{x}}- \frac{\sqrt{3}}{6}a \left(x_{14} - 2 y_{14} + z_{14}\right) \,\mathbf{\hat{y}}+\frac{1}{6}c \left(2 x_{14} + 2 y_{14} + 2 z_{14} + 3\right) \,\mathbf{\hat{z}}$ | (6b) | O III |
| $\mathbf{B_{71}}$ | = | $\left(y_{14} + \frac{1}{2}\right) \, \mathbf{a}_{1}+\left(x_{14} + \frac{1}{2}\right) \, \mathbf{a}_{2}+\left(z_{14} + \frac{1}{2}\right) \, \mathbf{a}_{3}$ | = | $\frac{1}{2}a \left(y_{14} - z_{14}\right) \,\mathbf{\hat{x}}+\frac{\sqrt{3}}{6}a \left(2 x_{14} - y_{14} - z_{14}\right) \,\mathbf{\hat{y}}+\frac{1}{6}c \left(2 x_{14} + 2 y_{14} + 2 z_{14} + 3\right) \,\mathbf{\hat{z}}$ | (6b) | O III |
| $\mathbf{B_{72}}$ | = | $\left(x_{14} + \frac{1}{2}\right) \, \mathbf{a}_{1}+\left(z_{14} + \frac{1}{2}\right) \, \mathbf{a}_{2}+\left(y_{14} + \frac{1}{2}\right) \, \mathbf{a}_{3}$ | = | $\frac{1}{2}a \left(x_{14} - y_{14}\right) \,\mathbf{\hat{x}}- \frac{\sqrt{3}}{6}a \left(x_{14} + y_{14} - 2 z_{14}\right) \,\mathbf{\hat{y}}+\frac{1}{6}c \left(2 x_{14} + 2 y_{14} + 2 z_{14} + 3\right) \,\mathbf{\hat{z}}$ | (6b) | O III |
| $\mathbf{B_{73}}$ | = | $x_{15} \, \mathbf{a}_{1}+y_{15} \, \mathbf{a}_{2}+z_{15} \, \mathbf{a}_{3}$ | = | $\frac{1}{2}a \left(x_{15} - z_{15}\right) \,\mathbf{\hat{x}}- \frac{\sqrt{3}}{6}a \left(x_{15} - 2 y_{15} + z_{15}\right) \,\mathbf{\hat{y}}+\frac{1}{3}c \left(x_{15} + y_{15} + z_{15}\right) \,\mathbf{\hat{z}}$ | (6b) | O IV |
| $\mathbf{B_{74}}$ | = | $z_{15} \, \mathbf{a}_{1}+x_{15} \, \mathbf{a}_{2}+y_{15} \, \mathbf{a}_{3}$ | = | $- \frac{1}{2}a \left(y_{15} - z_{15}\right) \,\mathbf{\hat{x}}+\frac{\sqrt{3}}{6}a \left(2 x_{15} - y_{15} - z_{15}\right) \,\mathbf{\hat{y}}+\frac{1}{3}c \left(x_{15} + y_{15} + z_{15}\right) \,\mathbf{\hat{z}}$ | (6b) | O IV |
| $\mathbf{B_{75}}$ | = | $y_{15} \, \mathbf{a}_{1}+z_{15} \, \mathbf{a}_{2}+x_{15} \, \mathbf{a}_{3}$ | = | $- \frac{1}{2}a \left(x_{15} - y_{15}\right) \,\mathbf{\hat{x}}- \frac{\sqrt{3}}{6}a \left(x_{15} + y_{15} - 2 z_{15}\right) \,\mathbf{\hat{y}}+\frac{1}{3}c \left(x_{15} + y_{15} + z_{15}\right) \,\mathbf{\hat{z}}$ | (6b) | O IV |
| $\mathbf{B_{76}}$ | = | $\left(z_{15} + \frac{1}{2}\right) \, \mathbf{a}_{1}+\left(y_{15} + \frac{1}{2}\right) \, \mathbf{a}_{2}+\left(x_{15} + \frac{1}{2}\right) \, \mathbf{a}_{3}$ | = | $- \frac{1}{2}a \left(x_{15} - z_{15}\right) \,\mathbf{\hat{x}}- \frac{\sqrt{3}}{6}a \left(x_{15} - 2 y_{15} + z_{15}\right) \,\mathbf{\hat{y}}+\frac{1}{6}c \left(2 x_{15} + 2 y_{15} + 2 z_{15} + 3\right) \,\mathbf{\hat{z}}$ | (6b) | O IV |
| $\mathbf{B_{77}}$ | = | $\left(y_{15} + \frac{1}{2}\right) \, \mathbf{a}_{1}+\left(x_{15} + \frac{1}{2}\right) \, \mathbf{a}_{2}+\left(z_{15} + \frac{1}{2}\right) \, \mathbf{a}_{3}$ | = | $\frac{1}{2}a \left(y_{15} - z_{15}\right) \,\mathbf{\hat{x}}+\frac{\sqrt{3}}{6}a \left(2 x_{15} - y_{15} - z_{15}\right) \,\mathbf{\hat{y}}+\frac{1}{6}c \left(2 x_{15} + 2 y_{15} + 2 z_{15} + 3\right) \,\mathbf{\hat{z}}$ | (6b) | O IV |
| $\mathbf{B_{78}}$ | = | $\left(x_{15} + \frac{1}{2}\right) \, \mathbf{a}_{1}+\left(z_{15} + \frac{1}{2}\right) \, \mathbf{a}_{2}+\left(y_{15} + \frac{1}{2}\right) \, \mathbf{a}_{3}$ | = | $\frac{1}{2}a \left(x_{15} - y_{15}\right) \,\mathbf{\hat{x}}- \frac{\sqrt{3}}{6}a \left(x_{15} + y_{15} - 2 z_{15}\right) \,\mathbf{\hat{y}}+\frac{1}{6}c \left(2 x_{15} + 2 y_{15} + 2 z_{15} + 3\right) \,\mathbf{\hat{z}}$ | (6b) | O IV |
| $\mathbf{B_{79}}$ | = | $x_{16} \, \mathbf{a}_{1}+y_{16} \, \mathbf{a}_{2}+z_{16} \, \mathbf{a}_{3}$ | = | $\frac{1}{2}a \left(x_{16} - z_{16}\right) \,\mathbf{\hat{x}}- \frac{\sqrt{3}}{6}a \left(x_{16} - 2 y_{16} + z_{16}\right) \,\mathbf{\hat{y}}+\frac{1}{3}c \left(x_{16} + y_{16} + z_{16}\right) \,\mathbf{\hat{z}}$ | (6b) | O V |
| $\mathbf{B_{80}}$ | = | $z_{16} \, \mathbf{a}_{1}+x_{16} \, \mathbf{a}_{2}+y_{16} \, \mathbf{a}_{3}$ | = | $- \frac{1}{2}a \left(y_{16} - z_{16}\right) \,\mathbf{\hat{x}}+\frac{\sqrt{3}}{6}a \left(2 x_{16} - y_{16} - z_{16}\right) \,\mathbf{\hat{y}}+\frac{1}{3}c \left(x_{16} + y_{16} + z_{16}\right) \,\mathbf{\hat{z}}$ | (6b) | O V |
| $\mathbf{B_{81}}$ | = | $y_{16} \, \mathbf{a}_{1}+z_{16} \, \mathbf{a}_{2}+x_{16} \, \mathbf{a}_{3}$ | = | $- \frac{1}{2}a \left(x_{16} - y_{16}\right) \,\mathbf{\hat{x}}- \frac{\sqrt{3}}{6}a \left(x_{16} + y_{16} - 2 z_{16}\right) \,\mathbf{\hat{y}}+\frac{1}{3}c \left(x_{16} + y_{16} + z_{16}\right) \,\mathbf{\hat{z}}$ | (6b) | O V |
| $\mathbf{B_{82}}$ | = | $\left(z_{16} + \frac{1}{2}\right) \, \mathbf{a}_{1}+\left(y_{16} + \frac{1}{2}\right) \, \mathbf{a}_{2}+\left(x_{16} + \frac{1}{2}\right) \, \mathbf{a}_{3}$ | = | $- \frac{1}{2}a \left(x_{16} - z_{16}\right) \,\mathbf{\hat{x}}- \frac{\sqrt{3}}{6}a \left(x_{16} - 2 y_{16} + z_{16}\right) \,\mathbf{\hat{y}}+\frac{1}{6}c \left(2 x_{16} + 2 y_{16} + 2 z_{16} + 3\right) \,\mathbf{\hat{z}}$ | (6b) | O V |
| $\mathbf{B_{83}}$ | = | $\left(y_{16} + \frac{1}{2}\right) \, \mathbf{a}_{1}+\left(x_{16} + \frac{1}{2}\right) \, \mathbf{a}_{2}+\left(z_{16} + \frac{1}{2}\right) \, \mathbf{a}_{3}$ | = | $\frac{1}{2}a \left(y_{16} - z_{16}\right) \,\mathbf{\hat{x}}+\frac{\sqrt{3}}{6}a \left(2 x_{16} - y_{16} - z_{16}\right) \,\mathbf{\hat{y}}+\frac{1}{6}c \left(2 x_{16} + 2 y_{16} + 2 z_{16} + 3\right) \,\mathbf{\hat{z}}$ | (6b) | O V |
| $\mathbf{B_{84}}$ | = | $\left(x_{16} + \frac{1}{2}\right) \, \mathbf{a}_{1}+\left(z_{16} + \frac{1}{2}\right) \, \mathbf{a}_{2}+\left(y_{16} + \frac{1}{2}\right) \, \mathbf{a}_{3}$ | = | $\frac{1}{2}a \left(x_{16} - y_{16}\right) \,\mathbf{\hat{x}}- \frac{\sqrt{3}}{6}a \left(x_{16} + y_{16} - 2 z_{16}\right) \,\mathbf{\hat{y}}+\frac{1}{6}c \left(2 x_{16} + 2 y_{16} + 2 z_{16} + 3\right) \,\mathbf{\hat{z}}$ | (6b) | O V |
| $\mathbf{B_{85}}$ | = | $x_{17} \, \mathbf{a}_{1}+y_{17} \, \mathbf{a}_{2}+z_{17} \, \mathbf{a}_{3}$ | = | $\frac{1}{2}a \left(x_{17} - z_{17}\right) \,\mathbf{\hat{x}}- \frac{\sqrt{3}}{6}a \left(x_{17} - 2 y_{17} + z_{17}\right) \,\mathbf{\hat{y}}+\frac{1}{3}c \left(x_{17} + y_{17} + z_{17}\right) \,\mathbf{\hat{z}}$ | (6b) | O VI |
| $\mathbf{B_{86}}$ | = | $z_{17} \, \mathbf{a}_{1}+x_{17} \, \mathbf{a}_{2}+y_{17} \, \mathbf{a}_{3}$ | = | $- \frac{1}{2}a \left(y_{17} - z_{17}\right) \,\mathbf{\hat{x}}+\frac{\sqrt{3}}{6}a \left(2 x_{17} - y_{17} - z_{17}\right) \,\mathbf{\hat{y}}+\frac{1}{3}c \left(x_{17} + y_{17} + z_{17}\right) \,\mathbf{\hat{z}}$ | (6b) | O VI |
| $\mathbf{B_{87}}$ | = | $y_{17} \, \mathbf{a}_{1}+z_{17} \, \mathbf{a}_{2}+x_{17} \, \mathbf{a}_{3}$ | = | $- \frac{1}{2}a \left(x_{17} - y_{17}\right) \,\mathbf{\hat{x}}- \frac{\sqrt{3}}{6}a \left(x_{17} + y_{17} - 2 z_{17}\right) \,\mathbf{\hat{y}}+\frac{1}{3}c \left(x_{17} + y_{17} + z_{17}\right) \,\mathbf{\hat{z}}$ | (6b) | O VI |
| $\mathbf{B_{88}}$ | = | $\left(z_{17} + \frac{1}{2}\right) \, \mathbf{a}_{1}+\left(y_{17} + \frac{1}{2}\right) \, \mathbf{a}_{2}+\left(x_{17} + \frac{1}{2}\right) \, \mathbf{a}_{3}$ | = | $- \frac{1}{2}a \left(x_{17} - z_{17}\right) \,\mathbf{\hat{x}}- \frac{\sqrt{3}}{6}a \left(x_{17} - 2 y_{17} + z_{17}\right) \,\mathbf{\hat{y}}+\frac{1}{6}c \left(2 x_{17} + 2 y_{17} + 2 z_{17} + 3\right) \,\mathbf{\hat{z}}$ | (6b) | O VI |
| $\mathbf{B_{89}}$ | = | $\left(y_{17} + \frac{1}{2}\right) \, \mathbf{a}_{1}+\left(x_{17} + \frac{1}{2}\right) \, \mathbf{a}_{2}+\left(z_{17} + \frac{1}{2}\right) \, \mathbf{a}_{3}$ | = | $\frac{1}{2}a \left(y_{17} - z_{17}\right) \,\mathbf{\hat{x}}+\frac{\sqrt{3}}{6}a \left(2 x_{17} - y_{17} - z_{17}\right) \,\mathbf{\hat{y}}+\frac{1}{6}c \left(2 x_{17} + 2 y_{17} + 2 z_{17} + 3\right) \,\mathbf{\hat{z}}$ | (6b) | O VI |
| $\mathbf{B_{90}}$ | = | $\left(x_{17} + \frac{1}{2}\right) \, \mathbf{a}_{1}+\left(z_{17} + \frac{1}{2}\right) \, \mathbf{a}_{2}+\left(y_{17} + \frac{1}{2}\right) \, \mathbf{a}_{3}$ | = | $\frac{1}{2}a \left(x_{17} - y_{17}\right) \,\mathbf{\hat{x}}- \frac{\sqrt{3}}{6}a \left(x_{17} + y_{17} - 2 z_{17}\right) \,\mathbf{\hat{y}}+\frac{1}{6}c \left(2 x_{17} + 2 y_{17} + 2 z_{17} + 3\right) \,\mathbf{\hat{z}}$ | (6b) | O VI |
| $\mathbf{B_{91}}$ | = | $x_{18} \, \mathbf{a}_{1}+y_{18} \, \mathbf{a}_{2}+z_{18} \, \mathbf{a}_{3}$ | = | $\frac{1}{2}a \left(x_{18} - z_{18}\right) \,\mathbf{\hat{x}}- \frac{\sqrt{3}}{6}a \left(x_{18} - 2 y_{18} + z_{18}\right) \,\mathbf{\hat{y}}+\frac{1}{3}c \left(x_{18} + y_{18} + z_{18}\right) \,\mathbf{\hat{z}}$ | (6b) | O VII |
| $\mathbf{B_{92}}$ | = | $z_{18} \, \mathbf{a}_{1}+x_{18} \, \mathbf{a}_{2}+y_{18} \, \mathbf{a}_{3}$ | = | $- \frac{1}{2}a \left(y_{18} - z_{18}\right) \,\mathbf{\hat{x}}+\frac{\sqrt{3}}{6}a \left(2 x_{18} - y_{18} - z_{18}\right) \,\mathbf{\hat{y}}+\frac{1}{3}c \left(x_{18} + y_{18} + z_{18}\right) \,\mathbf{\hat{z}}$ | (6b) | O VII |
| $\mathbf{B_{93}}$ | = | $y_{18} \, \mathbf{a}_{1}+z_{18} \, \mathbf{a}_{2}+x_{18} \, \mathbf{a}_{3}$ | = | $- \frac{1}{2}a \left(x_{18} - y_{18}\right) \,\mathbf{\hat{x}}- \frac{\sqrt{3}}{6}a \left(x_{18} + y_{18} - 2 z_{18}\right) \,\mathbf{\hat{y}}+\frac{1}{3}c \left(x_{18} + y_{18} + z_{18}\right) \,\mathbf{\hat{z}}$ | (6b) | O VII |
| $\mathbf{B_{94}}$ | = | $\left(z_{18} + \frac{1}{2}\right) \, \mathbf{a}_{1}+\left(y_{18} + \frac{1}{2}\right) \, \mathbf{a}_{2}+\left(x_{18} + \frac{1}{2}\right) \, \mathbf{a}_{3}$ | = | $- \frac{1}{2}a \left(x_{18} - z_{18}\right) \,\mathbf{\hat{x}}- \frac{\sqrt{3}}{6}a \left(x_{18} - 2 y_{18} + z_{18}\right) \,\mathbf{\hat{y}}+\frac{1}{6}c \left(2 x_{18} + 2 y_{18} + 2 z_{18} + 3\right) \,\mathbf{\hat{z}}$ | (6b) | O VII |
| $\mathbf{B_{95}}$ | = | $\left(y_{18} + \frac{1}{2}\right) \, \mathbf{a}_{1}+\left(x_{18} + \frac{1}{2}\right) \, \mathbf{a}_{2}+\left(z_{18} + \frac{1}{2}\right) \, \mathbf{a}_{3}$ | = | $\frac{1}{2}a \left(y_{18} - z_{18}\right) \,\mathbf{\hat{x}}+\frac{\sqrt{3}}{6}a \left(2 x_{18} - y_{18} - z_{18}\right) \,\mathbf{\hat{y}}+\frac{1}{6}c \left(2 x_{18} + 2 y_{18} + 2 z_{18} + 3\right) \,\mathbf{\hat{z}}$ | (6b) | O VII |
| $\mathbf{B_{96}}$ | = | $\left(x_{18} + \frac{1}{2}\right) \, \mathbf{a}_{1}+\left(z_{18} + \frac{1}{2}\right) \, \mathbf{a}_{2}+\left(y_{18} + \frac{1}{2}\right) \, \mathbf{a}_{3}$ | = | $\frac{1}{2}a \left(x_{18} - y_{18}\right) \,\mathbf{\hat{x}}- \frac{\sqrt{3}}{6}a \left(x_{18} + y_{18} - 2 z_{18}\right) \,\mathbf{\hat{y}}+\frac{1}{6}c \left(2 x_{18} + 2 y_{18} + 2 z_{18} + 3\right) \,\mathbf{\hat{z}}$ | (6b) | O VII |
References
- I. Huskić, I. V. Pekov, S. V. Krivovichev, and T. Friščić, Minerals with metal-organic framework structures, Sci. Adv. 2, 1600621 (2016), doi:10.1126/sciadv.1600621.
Prototype Generator
aflow --proto=A6BC18DEF21_hR96_161_2b_a_6b_a_a_7b --params=$a,c/a,x_{1},x_{2},x_{3},x_{4},y_{4},z_{4},x_{5},y_{5},z_{5},x_{6},y_{6},z_{6},x_{7},y_{7},z_{7},x_{8},y_{8},z_{8},x_{9},y_{9},z_{9},x_{10},y_{10},z_{10},x_{11},y_{11},z_{11},x_{12},y_{12},z_{12},x_{13},y_{13},z_{13},x_{14},y_{14},z_{14},x_{15},y_{15},z_{15},x_{16},y_{16},z_{16},x_{17},y_{17},z_{17},x_{18},y_{18},z_{18}$
